함수 F가 있을때 F(x) = x가 되는 x를 고정점이라 한다. 아래 그림은 3개의 고정점이 존재한다.
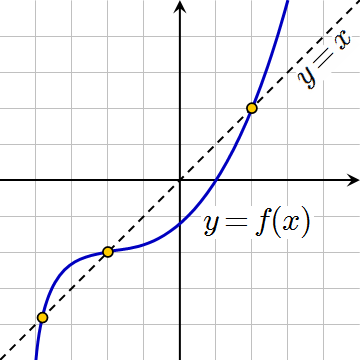
함수 F에 대해 임의의 x에서 시작하여  식으로 반복될때 x가 고정점으로 수렴하면 이 고정점을 attractive fixed point라고 한다. attractive fixed point가 아니면 초기값을 잘 설정해야 한다.
식으로 반복될때 x가 고정점으로 수렴하면 이 고정점을 attractive fixed point라고 한다. attractive fixed point가 아니면 초기값을 잘 설정해야 한다.
함수 F(x)의 근을 찾는 문제는 F(x)=0 을 x=g(x) 식으로 변경할 후 g(x)의 고정점을 찾는 문제로 바꿀 수 있다. 고정점을 찾는 방법은 초기값 x0가 주어지면 x1=g(x0), x2=g(x1), x3=g(x2),... 로 반복해서 계산되고, 계산 중 xn과 x(n-1)의 차이가 tolerance 이하가 될 때까지 반복하면 된다.
어떤 문제를 고정점을 찾는 문제로 바꾼다는 것은 mathematical analysis의 문제를 numerical analysis의 문제로 바꾼다는 것을 뜻하며, 이는 결국 알고리즘을 통한 근사치를 계산하는 문제로 바꾸는 것을 의미하게 된다. 쉽게 얘기해서 컴퓨터 프로그래밍으로 풀 수 있는 문제가 된다는 뜻이다. 이와 유사한 개념이 Taylor series로 이는 f(x)를 멱급수(power series)로 표현하여 근사치를 계산하는 방법이다.
어떤 수 a에 대한 square-root을 값을 찾는 문제를 보면, x=sqrt(a) 이면 이는 x^2=a 와 동일하고 이는 x=a/x 가 되므로 a/x의 고정점을 찾는 문제로 풀 수 있다. a의 값에 따라 써 보면, a=2 이면 sqrt(2)을 푸는 문제로 이는 y=2/x의 고정점이 되고 , a=3 이면 y=3/x의 고정점을 찾는 문제가 된다.







