주소 : http://inst.eecs.berkeley.edu/~scheme/
UC Berkeley의 CS61A(SICP) 강의에서 사용되는 Scheme. STk 의 수정버전이라고 하는데, 자세히는 모름. CS 강의에서 사용하기 위해 수정되어 있어, 책의 코드들을 실행하는데 모듈들이 포함되어 있음.
SICP 공부할때는 Racket 보다는 좋을듯 한데, 문제는 GUI REPL이 없다는 점. 일단 emacs의 inferior-scheme과 scheme-mode를 사용하면 좋을듯.
(require (planet "sicp-concurrency.ss" ("dyoo" "sicp-concurrency.plt" 1 1)))
티스토리에 소스를 올리는게 넘 불편해서 github repository를 하나 만들었습니다. 앞으로 소스 코드는 여기에 올리는게 어떨지? 이참에 분산 VCS인 git에 대해서도 알아보는건? ^^
커밋을 하려면 github에 가입하고도, 몇 가지 준비가 필요하니 한번 논의해 보시죠.
HTML 편집 모드에서 아래와 같이 <pre class="brush:scheme">와 </pre> 사이에 Scheme 코드를 입력하면 예쁘게 출력된다.
<pre class="brush:scheme">
;; ex 1.12 pascal's triangle
;; p(r, c) = p(r-1, c-1) + p(r-1, c)
;; p(r, 1) = 1, p(r, r) = 1
(define (pt r c)
(cond ((or (= c 1) (= r c)) 1)
((or (< c 0) (< r 0) (> c r)) 0)
(else (+ (pt (- r 1) (- c 1))
(pt (- r 1) c)))))
</pre>
;; ex 1.12 pascal's triangle
;; p(r, c) = p(r-1, c-1) + p(r-1, c)
;; p(r, 1) = 1, p(r, r) = 1
(define (pt r c)
(cond ((or (= c 1) (= r c)) 1)
((or (< c 0) (< r 0) (> c r)) 0)
(else (+ (pt (- r 1) (- c 1))
(pt (- r 1) c)))))
* > 또는 < 를 제대로 rendering 못하는 버그 있음. 위 pascal's triangle 코드의 6번째 줄에서 < 가 <; 로 출력되고 있음.
함수 F가 있을때 F(x) = x가 되는 x를 고정점이라 한다. 아래 그림은 3개의 고정점이 존재한다.
함수 F에 대해 임의의 x에서 시작하여 
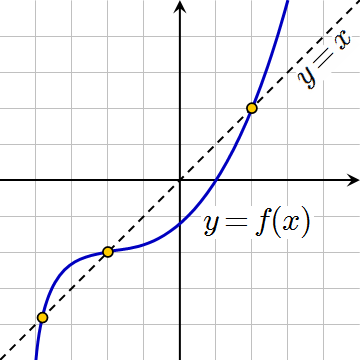
식으로 반복될때 x가 고정점으로 수렴하면 이 고정점을 attractive fixed point라고 한다. attractive fixed point가 아니면 초기값을 잘 설정해야 한다.
함수 F(x)의 근을 찾는 문제는 F(x)=0 을 x=g(x) 식으로 변경할 후 g(x)의 고정점을 찾는 문제로 바꿀 수 있다. 고정점을 찾는 방법은 초기값 x0가 주어지면 x1=g(x0), x2=g(x1), x3=g(x2),... 로 반복해서 계산되고, 계산 중 xn과 x(n-1)의 차이가 tolerance 이하가 될 때까지 반복하면 된다.
어떤 문제를 고정점을 찾는 문제로 바꾼다는 것은 mathematical analysis의 문제를 numerical analysis의 문제로 바꾼다는 것을 뜻하며, 이는 결국 알고리즘을 통한 근사치를 계산하는 문제로 바꾸는 것을 의미하게 된다. 쉽게 얘기해서 컴퓨터 프로그래밍으로 풀 수 있는 문제가 된다는 뜻이다. 이와 유사한 개념이 Taylor series로 이는 f(x)를 멱급수(power series)로 표현하여 근사치를 계산하는 방법이다.
어떤 수 a에 대한 square-root을 값을 찾는 문제를 보면, x=sqrt(a) 이면 이는 x^2=a 와 동일하고 이는 x=a/x 가 되므로 a/x의 고정점을 찾는 문제로 풀 수 있다. a의 값에 따라 써 보면, a=2 이면 sqrt(2)을 푸는 문제로 이는 y=2/x의 고정점이 되고 , a=3 이면 y=3/x의 고정점을 찾는 문제가 된다.
|
